‍

For the last month we've been hard at work adding a new feature to Elodin, an ultra-high-speed implementation of EGM2008. EGM2008 – or Earth Gravitational Model 2008 for those acronym phobic readers – a high precision model of Earth's gravitational field.. What once required significant computational resources can now run in milliseconds, unlocking new possibilities for satellite missions, constellation management, and more.

‍

You’d think we could stick to Newton’s classic gravity model (aka the Coulomb model) to explain everything about Earth’s gravitational field. It’d be great if it were that simple, but planetary gravity is far messier. Earth isn’t a perfectly smooth, uniformly dense sphere; it’s more like a slightly squished ball (an oblate spheroid) with bumps and dips from mountains, ocean trenches, and uneven internal mass distribution. So early on (before the space age), scientists began measuring Earth’s gravitational field - using ground-based techniques like pendulum experiments. Though pendulums provided more accuracy than the coulomb model, in order to get accurate enough data for something as simple as an orbit simulation, the pendulums would be unfathomably massive.

‍

That all started to change in 1957 with the launch of Sputnik I, the first satellite to reveal how gravity could be studied through its effects on orbits. Early missions like Vanguard and Transit laid the groundwork, giving scientists basic estimates of Earth’s gravity. But the technology of the time had its limits—data was sparse, and computers were primitive. Over the years, advanced satellites like Topex/Poseidon and Lageos brought more detailed and accurate measurements, transforming our understanding of Earth’s gravitational quirks.

‍

Fast forward to today, and EGM2008 is the cornerstone of high-precision gravity models. It accounts for every bump and dip, every subtle anomaly in Earth’s gravity field, capturing details earlier methods could never achieve. A big part of this leap forward came from GRACE (Gravity Recovery and Climate Experiment) satellites. Launched in 2002, GRACE used twin satellites to measure tiny variations in Earth’s gravity by tracking the distance between them as they orbited the planet. These variations revealed shifts in mass—whether from melting ice caps, ocean currents, or changes in groundwater. GRACE provided an unprecedented view of how gravity changes over time and space, feeding crucial data into the EGM2008 model. Combined with data from earlier missions like Topex/Poseidon and Lageos, GRACE helped create a model that doesn’t just map Earth’s gravity—it tells the story of its dynamic changes.

‍

But how does EGM2008 actually work? ‍
EGM2008 uses spherical harmonics, a mathematical tool that models Earth’s gravity field with remarkable precision. These harmonics originate from mathematics and mathematical physics, specifically as solutions to Laplace’s equation. They allow the gravity field to be broken into components of different “degrees” and “orders,” with each degree and order representing a level of detail or “frequency” in the field. If you look at the visualization of these mathematical models, it makes perfect sense—they map peaks and valleys across a semi-spherical surface with uncanny precision.

To avoid reinventing the wheel, I looked for a library that already implemented EGM2008, but unfortunately, none could support real-time simulation effectively.  So I set off on a journey to implement the EGM2008 gravity model into our simulation platform. Like any good expedition team preparing for uncharted waters, I stocked up on critical supplies: energy drinks (far too many), research papers, and modern sea shanties (nothing helps me focus like the Interstellar soundtrack). After poring over four different academic papers, I decided to try implementing the approach outlined in one.

‍

My first attempt?
Pretty straightforward: take the math from the paper and translate it directly into code. Most of my time was spent decoding the intricate mathematical gymnastics Dr. Schaub and Dr. Martin performed in their equations. After a week of abusing energy drinks and wrecking my sleep schedule, I finally had a working gravity model. But when I tested it, disaster struck—the calculations were taking ~1.2 seconds for fidelity levels appropriate for a LEO satellite orbit. All that effort for an implementation slower than MATLAB? Unacceptable.

Determined to boost performance, I turned to some dark magic: JAX. I took another shot at implementing the paper’s math, this time “JAXified”. By replacing all the for loops with JAXs “fori” function, I hacked together a new implementation. The results? Marginal improvements—still far from acceptable. At this point, it seemed pointless to switch libraries or try another paper’s approach.

While marinating in defeat, I realized that the mathematical steps in the paper weren’t compatible with JAX’s optimizations, due to heavy use of conditionals and recursion (both big no-nos in JAX). The strength of JAX lies in its ability to perform vector computation, utilizing specialized instructions for simultaneous array operations. Recursion and conditional expressions, however, prevent the use of vectorization, resulting in slower execution. With this insight, I set out to reformulate the math to better align with JAX’s computation schemes. As I worked, I found even more areas to optimize. With a new mission plan, I dove in.

First, I reformulated all the math to use array operations (snippet of the reformulation is shown below). This way, I was able to swap out for-loops for combinations of JAX’s scan and vmap functions and compute the addend of these summation blocks by using traditional array operations rather than traversing through them and doing element by element scalar operations

Finally, I replaced all conditional execution with precomputed steps or JAX-friendly conditional blocks. Sounds simple enough, right? (Hint: it wasn’t.) It took an entire weekend to reformulate the math and another week of 10- to 12-hour days to implement it. But in the end, I had a working model. Not just any model—my implementation wasn’t just a few milliseconds faster than others. It was orders of magnitude faster.

Benchmarking revealed that we are the only available platform capable of simulating gravity using the EGM2008 model at full resolution in real time. That means our platform doesn’t just simulate satellite orbits in real time—it can simulate entire constellations on a laptop. Who’s the fastest kid on the block now, MATLAB? 

‍

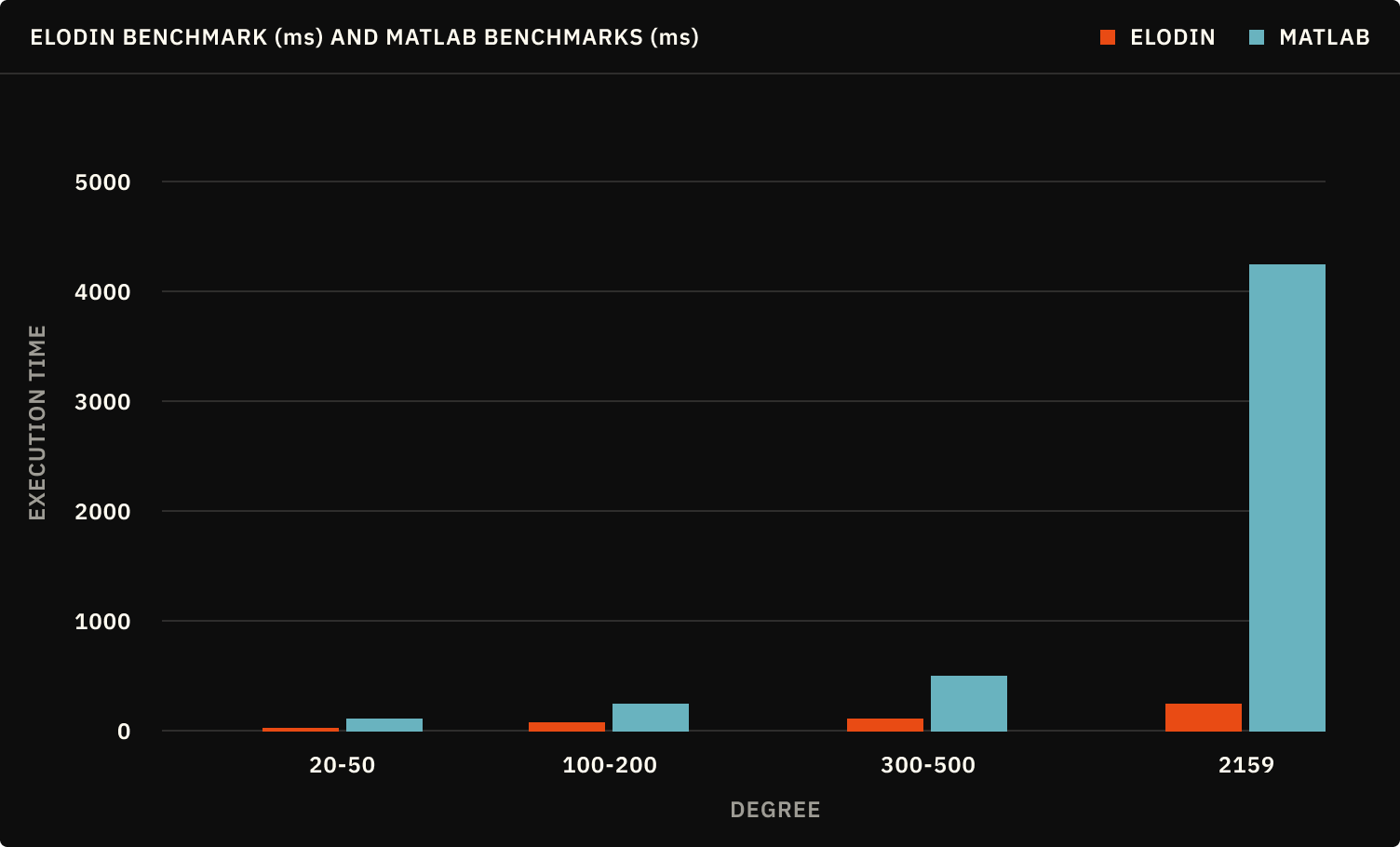
If being blazing fast wasn’t enough, our library is easy to use as well. Typically EGM models are very hard to use – they are embedded in proprietary software and hard to integrate with your existing software stack. Elodin has solved this by exposing our EGM model through a simple Python interface:

‍

gravity_model = egm08.EGM08(defree = 2159, use_j2= False)
gravity_force_vector = gravity_model.compute_field(pos_x, pos_y, pos_z, mass)

‍

This breakthrough opens up a whole new world for space simulations, enabling applications like constellation planning, space debris management, fuel budgeting, and control system design. The possibilities are endless, and we’re just getting started. We’re excited to see how people can use our platform's newest addition to tackle new challenges.